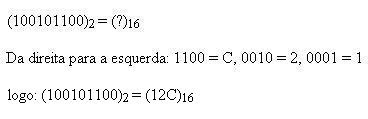Curiosidades - Sistema Decimal

Como já foi dito no sistema romano, haviam problemas em somar,subtrair,dividir e multiplicar, problemas que haviam tambem nos outros sistemas numéricos primitivos.



Imaginaram como era dificil? Só começou a ficar mais fácil com a descoberta do sistema indiano de contar. O sistema numérico indiano, também chamado de hindu, não utilizava figuras ou letras para representar números. No início, ele era formado por nove símbolos, que representavam de um a nove. Depois, há cerca de 2.600 anos atrás, eles criaram um décimo símbolo, para representar o vazio.

Alem de criarem um novo sistema numérico ele também era um sistema numérico Posicional. Como já foi explicado antes, como funcionam os sistemas numéricos posicionais, vou continuar... caso haja dúvidas olhem o post:
http://interligados2009.blogspot.com/2009/03/nao-usaremos-o-sistema-romano-pois-ele.html

Continuando... também existia símbolo para o zero, e os agrupamentos em dez e a leitura pela posição dos números. Esta era a chave do sucesso do sistema indiano. Ele foi, por muito tempo, de uso exclusivo deste povo. Entretanto, isto mudaria por causa da curiosidade de um certo matemático árabe.

Seu nome era Al-Khowarizmi. Ele estudou por muito tempo a matemática indiana. Percebeu o quanto o sistema indiano facilitava cálculos e, ao mesmo tempo, o quanto era simples. Um sistema fantástico, que todos deveriam aprender. E foi por isso que Al-Khowarizmi escreveu o livro Sobre a arte hindu de calcular. Queria contar aquela novidade ao mundo.

Com o livro, matemáticos de todas as partes ficaram por dentro dos estudos do sábio árabe. Os símbolos 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9 ficaram conhecidos como a notação de Al-Khowarizmi. Daí o nome algarismo, forma latina de falar o nome árabe.



Os símbolos inventados pelos indianos e divulgados pelos árabes são os números que utilizamos hoje. Por isso, eles formam o chamado sistema indo-arábico de numeração.

Quem nunca tentou contar, subtrair ou somar algum número com os dedos? ou ainda falamos tanto sobre Árabe e Hindu, e porque de decimal?

O nome decimal surgiu a partir da contagem de 10 em 10 e como possuímos 10 dedos nas mãos, dedo em latim significa dígitos e o sistema tem 10 possui dígitos/símbolos. Torno-se usual a nomeclatura Decimal para representação do sistema Indu-Arábico.

Como você pôde ver também algumas coisas nunca mudam... como fazer contas com os dedos!

Fonte:
http://www.invivo.fiocruz.br/cgi/cgilua.exe/sys/start.htm?infoid=984&sid=9

E-mail/Msn/Orkut: oguh-headshot@hotmail.com


Dúvidas/Sugestões/Idéias/ e Novidades sobre o que virá

Curiosidades - Sistema Numérico Romano

Hoje vi a professora de Fundamentos da Álgebra para Computação escrevendo aqueles símbolos, então ela comentou que ali eram Romanos em minúsculo quando alguem lhe perguntou (eu imaginava tudo menos romano... até complexo cheguei a pensar.)

Então para aqueles que gostam, ou ainda tem pouco conhecimento ou ainda querem conhecer, esse sistema que é amplamente usado há vários anos, que nos dias atuais é mais usado em capítulos de lívros ou em representações matemáticas. Conheçam a história desse sistema.

Com o crescimento do império romano, houve uma necessidade da criação de números, que hoje em dia são conhecidos por nós em letras, como:
I(1)
V(5)
X(10)
L(50)
C(100)
D(500)
M(1000)

Os quais antes eram conhecidos como:



Alguns devem estar se perguntando como esses símbolos viraram essas letras que nós conhecemos, então mostrarei como foi a evolução do 50 , até o L que conhecemos:



Eles usavam esses números de maneira bem interessante, pois se um valor menor estivesse a direita do valor maior somava-se com o maior, caso ele estivesse a esquerda subtraía-se

Direita:
VI (5 + 1) = 6
XII (10 + 2) = 12
LIII (50 + 3) = 53
CX (100 + 10) = 110

Esquerda:
IV (5 – 1) = 4
IX (10 – 1) = 9
XL (50 – 10) = 40
XC (100 – 10) = 90
CD (500 – 100) = 400
CM (1000 – 100) = 900

Em tempos mais antigos os romanos escreviam IIII para representar a quantidade 4 e VIIII para representar 9. Com o passar dos anos adotaram a esquerda subtrai-se e a direita soma-se.

Quando trabalhava-se na casa do Mil (M) havia umas complicações, pois como trabalhar com 20 mil? Escrever 20 M's? Eles adotaram um meio prático, eles passavam um traço encima da letra para multiplicar-lo por 1000.



Mas esta regra só se aplicava na multiplicação por mil. Por isso, ainda era muito trabalhoso representar alguns números em Roma. Você consegue ler o número abaixo?

MMMCMXCIX

Agora imagine somar e subtrair usando este número. Pior: multiplicar e dividir. Você arrisca? Nem os próprios romanos arriscavam fazer estas operações usando sua escrita numérica. Eles utilizavam outros meios, como os chamados ábacos, mesas onde desenhavam linhas que representavam ordens numéricas, movimentando fichas, que dependendo da posição no tabuleiro, representavam determinados valores.

Você imagina quem inventou o sistema decimal tão prático que utilizamos hoje para calcular? A solução desse mistério em breve surgirá rsrsrsrsrsrs.

Fonte:
http://www.invivo.fiocruz.br/cgi/cgilua.exe/sys/start.htm?infoid=983&sid=9

E-mail/Msn/Orkut: oguh-headshot@hotmail.com


Dúvidas/Sugestões/Idéias/ e Novidades sobre o que virá

Conversões (2)

Eis aqui mais Conversões..


1. Decimal/qualquer outra base

Para se obter a representação de uma quantidade no sistema decimal em qualquer outro sistema, é simples, se dá através de divisões sucessivas do número decimal pela base do sistema desejado. E, o resultado será os restos das divisões dispostos na ordem inversa.

Ex:

2. Outro sistema/Decimal

Esta conversão consiste da aplicação direta do TFN (Teorema Fundamental de Numeração), ou seja,

...+ X₃ x B³ + X₂ x B² + X₁ x B¹ + X₀ x B⁰ + X_-1 x B^-1 + X_-2 x B^-2 + X_-3 x B^-3 + ...


Ex:





3. Hexadecimal/Binário

Para converter um número hexadecimal em binário, substitui-se cada dígito hexadecimal por sua representação binária com quatro dígitos.

EX:


* A tabela a seguir mostra a equivalência entre os sistemas de numeração decimal, binário, octal e hexadecimal.




4. Binário/Hexadecimal

Para se converter de binário para hexadecimal, utiliza-se um procedimento inverso a conversão hexadecimal -> binário, ou seja, agrupa-se o número binário de 4 em 4 dígitos, da direita para a esquerda , e o substitui por seu equivalente hexadecimal.

Ex:

5. Binário/Octal

Muito semelhante ao método binário -> hexadecimal, contudo, neste caso, agrupa-se o número binário de 3 em 3 dígitos, da direita para a esquerda, e o substitui por seu equivalente octal.

Ex:

6. Octal/Binário

De modo muito semelhante a conversão hexadecimal -> binário, esta conversão substitui cada dígito octal por sua representação binária com três dígitos.

Ex:


7. Hexadecimal/Octal

Neste caso é necessário um passo intermediário: primeiro transforma-se o número hexadecimal em binário e então este é convertido em octal. Obtemos assim a seguinte equivalência para esta conversão: Hexadecimal -> Binário -> Octal.

Ex:

8. Octal/Hexadecimal

O mesmo acontece neste caso. Assim temos: Octal -> Binário -> Hexadecimal.

Ex:




http://www.lia.ufc.br/~paty/icc/notas/4/index.html (Profa. Patrícia Helaine L. Nascimento - e-mail: paty_landim@yahoo.com.br)


Aqui estão as conversões entre os sistemas de numeração!!
Muito simples!!
Qualquer dúvida, questionamento, curiosidade, enfim algo a acrescentar, é sempre bem vindo!!


Dúvidas/Sugestões/Idéias/ e Novidades sobre o que virá

Curiosidades - Sistema Numérico Grego

Como vimos, os Sistemas Romanos e Egípcios não são considerados sistemas posicionais, ou seja, não mudam de valor independente de onde eles estejam. Com o Sistema Numérico Grego, isso tambem acontece. Os gregos precisavam memorizar 27 letras. 9 letras representando unidades, 9 representando dezenas e 9 representando centenas. Observe a tabela abaixo:



Agora imaginem o numero 146. Ele corresponderia as seguintes letras:
rô(100)+mu(40)+digama(6) = 146

Para representar milhares, até menores que 10.000, fazia-se uma marca à esquerda da letra. Por exemplo:

5000 em numeração grega escreve-se ¢e(epsilon)

6751 em numeração grega escreve-se ¢V(digama) y(psi) n(nu) a(alfa) (6000+700+50+1);

9888 em numeração grega escreve-se ¢q(teta) w(ômega) p(pi) h(eta) (9000+800+80+8);

Para números superiores ou iguais a 10.000 usava-se a letra M para representar 10 milhares. Vejamos alguns exemplos:

10.000 em numeração grega escreve-se M elevado à a(alfa) (1*10.000);

20.000 em numeração grega escreve-se M elevado à b(beta) (2*10.000);

23.000 em numeração grega escreve-se M elevado à b(beta) 'g(gama) (2*10.000+3000);

71.750.000 em numeração grega escreve-se M elevado à (¢ z(zeta) r(rô) o(ômicron) e(epsilon)) ((7*1000+100+70+5)*10.000);

(OBS: essa numeração ta + organizada no link http://www.educ.fc.ul.pt/icm/icm99/icm36/numeracao_grega.htm )

Fonte:
http://www.invivo.fiocruz.br/cgi/cgilua.exe/sys/start.htm?infoid=985&sid=9
http://www.educ.fc.ul.pt/icm/icm99/icm36/numeracao_grega.htm

E-mail/Msn/Orkut: oguh-headshot@hotmail.com


Dúvidas/Sugestões/Idéias/ e Novidades sobre o que virá

Operações

Soma

Recordando as seguintes somas básicas:

1. 0+0=0
2. 0+1=1
3. 1+1=10

Assim, ao se somar 100110101 com 11010101, tem-se:

Opera-se como em decimal: no exemplo 1+1=10, então escreve-se 0 e "leva-se" 1. Soma-se este 1 à coluna seguinte: 1+0+0=1, e segue-se até terminar todas as colunas (exactamente como em decimal).

Subtração

A subtração ocorre de modo que quando temos 0 menos 1, precisamos "pedir emprestado" do elemento vizinho. Esse empréstimo vem valendo 2, pelo fato de ser um número binário (base 2). Então, no caso da coluna 0 - 1 = 1, porque na verdade a operação feita foi 2 - 1 = 1. Esse processo se repete e o elemento que cedeu o "empréstimo" e valia 1 passa a valer 0.

Produto

O produto de números binários é especialmente simples, já que o 0 multiplicado por qualquer coisa resulta 0, e o 1 é o elemento neutro do produto.

Por exemplo, a multiplicação de 10110 por 1001:





Exemplos em outras bases:









Muito fácil hein ... pratiquem!!!!!

Dúvidas, sugestões, questionamentos, curiosidades, é só falar....

Dúvidas/Sugestões/Idéias/ e Novidades sobre o que virá

Curiosidades - Matrix (O Filme)

Para muitos, matrix é apenas um filme, porém se você for buscar e aprofundar-se sobre esse assunto, notaria que muitas das coisas que acontecem no filme podem ser transformadas para a vida virtual, imaginando um sistema com toda sua organização e sincronismo e de repente alguns invasores tentam derrubar esse sistema.

Ex:
MetaCortex e a própria Matrix - Estrutura,Sistema Operacional.
Agentes smiths - Antivirus, Firewalls, Programas guardiões.
Neo,Morpheus e raça humana - Invasores, virus, etc.

O uso dos binários nas telas do filme matrix seria uma prova disso.

Fatos no filme que reforçam a idéia:

Demonstra a grande estrutura e eles seriam pequenos operários ou até mesmo pequenas partes do mesmo:
1- O mundo de Matrix é sonho. Pergunta Morpheu: “Você já teve um sonho, Neo, que parecia ser verdadeiro? E se você não conseguisse acordar desse sonho? Como você saberia a diferença entre o mundo dos sonhos e o mundo real?”. Nesse caso, o mundo só existe agora como parte de uma simulação neurointerativa (exclama Morpheu: “Você vivia num mundo de sonhos, Neo!”). E noutro lugar, Morpheus observa: “A Matrix é um mundo dos sonhos gerado por computador feito para nos controlar, para transformar o ser humano nisto aqui [bateria]”

Reforçam a idéia original, de invasores a estrutura em questão:
1- O discurso do agente Smith diante um Morpheu dopado é um libelo contra a civilização tecnológica (ironicamente dito por um representante-mor da Máquinas Inteligentes). Diz ele: “Os homens...vão para uma área e se multiplicam, até que todos os recursos naturais sejam consumidos. A única forma de sobreviverem é indo para uma outra área. Há um outro organismo neste Planeta que segue o mesmo padrão...Um vírus.” E arremata: “Os seres humanos são uma doença. Um câncer neste planeta. Vocês são uma praga!”.
2- Na trama de Matrix, o corpo, uma dimensão ineliminável da subjetividade humana é uma impossibilidade recorrente. Neo, Morpheus, Trinity e seu grupo, são entes digitais, programas-invasores do sistema de Matrix.

Conclusões:

Em Matrix, a realidade simulada é uma virtualização complexa espúria que oculta a verdadeira Realidade, o “deserto do Real”. De um lado, a bárbarie regressiva perto de 2199. De outro lado, o simulacro digital complexo que oculta a exploração – no sentido marxiano – do gênero humano pelas Máquinas Inteligentes. Estamos diante de um mundo digital, constituído de 0 e 1, um mundo binário, tão perfeito quanto a própria realidade concreta (no sentido da certeza sensível e da percepção, e mesmo do entendimento, empregando as categorias de Hegel). Neste mundo de Matrix, os objetos e pessoas são meros sistemas de códigos binários, programas de computador, deste imenso sistema informático.

Fonte:
http://www.telacritica.org/Matrix.htm

E-mail/Msn/Orkut: oguh-headshot@hotmail.com

Dúvidas/Sugestões/Idéias/ e Novidades sobre o que virá

Curiosidades - Sistema Numérico Egípcio

Criei esse post quando vi o antigo sistema numérico egípcio, e vi que nessa época eles já haviam feito algo similar ao sistema numérico romano.



Percebe-se que é bem similar aos romanos, pois soma-se todos os valores.

Olhando os números você deve ter se perguntado: por que representar o 1 com um traço vertical? E qual o significado do símbolo para 1.000?

Você tem algum palpite?
Existem muitas hipóteses. Uma delas é a que o símbolo para o 1 era um pedaço de corda estirado. Juntando vários desses pedaços nós ficamos com um pedaço maior, que se curva. Este pedaço de corda curvado era o símbolo para 10. Juntando mais pedaços de corda nós teríamos uma corda ainda maior, que poderia ser enrolada. O desenho de um rolinho de corda era o que representa 100.

Para representar 1.000 era utilizada a flor de lótus, símbolo da beleza. Para 10.000, os egípcios desenhavam o dedo do faraó, que representava poder; para 100.000, desenhavam um girino ou um sapo, que naquela cultura simbolizava fertilidade. E, finalmente, a representação de 1.000.000 era feita com a figura de um sacerdote louvando os deuses.

Fonte:
http://www.invivo.fiocruz.br/cgi/cgilua.exe/sys/start.htm?infoid=972&sid=9

E-mail/Msn/Orkut: oguh-headshot@hotmail.com

Dúvidas/Sugestões/Idéias/ e Novidades sobre o que virá

A Informação nos Computadores

Nós conseguimos guardar informações sob a forma de imagens e cenas;
Entretanto, o computador é uma máquina, sendo muito difícil construir circuitos para que ele guarde imagens, tal como o cérebro.
Então como é que as informações são manipuladas pelo computador?
A maneira mais fácil:

presença/ausência de sinal elétrico
Ligado/desligado
aceso/apagado
1/0

Como tem-se dois estados, chama-se essa representação de Codificação Binária.

A menor unidade que transita em um computador é o BIT que representa os estados aceso/apagado,
ligado/desligado, 1/0
Um símbolo, seja ele uma letra, um número, um sinal, é representado por um conjunto de bits.
A esse conjunto de Bits denomina-se BYTE
Tipicamente, 1 (um) Byte tem 8 (oito) Bits

Qualquer texto ou informação serão guardados no computador sob a forma de Arquivos de Dados.

Como o sistema de codificação é binário, as quantidades que representam grupos de bytes armazenados ou transportados no computador são potências de 2.

Assim:

1 KByte = 1.024 Bytes

1 MByte = 1.024 KBytes ou

1.048.576 Bytes

1 GByte = 1.024 MBytes ou

1.048.576 KBytes ou

1.073.741.824 Bytes

KByte = KiloByte = KB = K

MByte = MegaByte = MB = Mega

GByte = GigaByte = GB = Giga

Os dados e as informações em um computador são representados internamente das seguintes formas:

Representação Alfanumérica:

Representação ASCII: originalmente utilizava 7 bits, suficientes para representar 128 caracteres só serve para língua inglesa, pois não inclui acentos e símbolos utilizados em alguns idiomas, atualmente utiliza 8 bits, mas o problema da representação limitada continua;

Representação EBCDIC: assim como ASCII, também utilizava 7 bits inicialmente e hoje utiliza 8 bits usado

• nos mainframes IBM

• computadores Macintosh (Apple)

apesar de utilizar o mesmo número de bits que o ASCII, a representação de um símbolo difere nos dois códigos

Representação UNICODE: os códigos anteriores são insuficientes para representar símbolos de outros idiomas além do inglês este código amplia a representação para 16 bits, o que possibilita mais de 65.000 símbolos adotado por

• Apple, HP, IBM, Microsoft, Oracle, Sun,

Sybase, Unisys

Representação Numérica

Os códigos de caracteres não servem para representar números fracionários para esses números e para números muito grandes é usada a notação de ponto flutuante, os números são representados como potências de 2:

(-1)S x F x 2E , onde S = sinal

F = valor ponto flutuante

E = expoente

Precisão simples: 32 bits

Precisão dupla: 64 bits

Outras bases de representações

Algumas vezes são utilizadas outras bases de representação além da binária para facilitar a escrita. Bases mais usadas:

Hexadecimal – base 16

Octal – base 8

www.geocities.com/locksmithone/classroom/sistemas_computacao/2007_1/lecture_slides/aula06.pdf


Olá pessoal, a partir das diversas informações que meus colegas já postaram no bolg, resolvi colocar um resuminho para que vocês se situem por inteiro no assunto...qualquer dúvida, questionamento, sugestão e curiosidades é só falar...

Dúvidas/Sugestões/Idéias/ e Novidades sobre o que virá aqui

Conversões Binários/Decimais

Sistema decimal
• O sistema de numeração que usamos no nosso
dia a dia é o sistema de numeração decimal ou de base dez
• Chama-se assim porque utiliza dez algarismos ou
dígitos: 0, 1, ...9
•Isto não acontece por acaso, utilizamos dez
dígitos porque temos dez dedos
•Com efeito, em latim a palavra dígito significa dedo

• No sistema decimal os números inteiros são representados
pela soma das suas unidades, dezenas, centenas, etc...
123 = 1 x 100 + 2 x 10 + 3 x 1
• É o mesmo que dizer que um número na base dez é
representado pela soma de várias potências de dez com
coeficientes indo de 0 a 9, inclusive

123(10) = 1 x 102+ 2 x 101+ 3 x 100
4321(10) = 4 x 103+ 3 x 102+ 2 x 101+ 1 x 100
98,76(10) = 9 x 101+ 8 x 100 + 7 x 10-1+ 6 x 10-2
-5,4 (10) = -5 x 100 - 4 x 10-1

Sistema binário

Um número na base dois é representado
pela soma de várias potências de dois com
coeficientes 0 ou 1

100(2) =1 x 22 + 0 x 21+0 x 20 =4(10)
101(2) =1 x 22 + 0 x 21+1 x 20 =5(10)
110(2) =1 x 22 + 1 x 21+0 x 20 =6(10)
111(2) =1 x 22 + 1 x 21+1 x 20 =7(10)

Perceba que a forma como construímos os
números no sistema binário é idêntica à forma como
o fazemos no sistema decimal, com a limitação de
dispormos apenas dos dígitos 0 e 1


*Construção dos números em decimal e Binário

base 10______base 2____base 10______base 2

*0__________0________*10_________1010
*1__________1________*11_________1011
*2__________10_______*12_________1100
*3__________11_______*13_________1101
*4__________100______*14_________1110
*5__________101______*15_________1111
*6__________110______*16_________10000
*7__________111______*17_________10001
*8__________1000_____*18_________10010

Legenda: *(decimal)

Conversão binário decimal

Um número converte-se da base 2 para a base 10
através da soma das várias potências de dois
multiplicadas pelos respectivos coeficientes.


Conversão decimal binário

Um número inteiro converte-se da base 10 para a base 2
utilizando o método das divisões sucessivas
•Divide-se o número e os sucessivos quocientes que forem
sendo obtidos por dois até o último quociente ser 0 ou 1
•Escrevem-se (da esquerda para a direita) o último
quociente e todos os restos (pela ordem inversa à que foram
obtidos)


Dúvidas/Sugestões/Idéias/ e Novidades sobre o que virá

ASCII - ANSI - UNICODE

Estranhei um pouco ninguem ter reparado ou comentado que a tabela ao lado se referia ao ANSI e não ao ASCII. Por isso resolvi criar este post para explicar o que significa ANSI e explicar o que significa Unicode.

O código de caracteres padrões hoje em dia são feitos em ASCII, mas descobriu-se que este tipo de representação só era adequado ao Ocidente(idiomas ocidentais), tornando-se bem populares nos países europeus. O grande problema deste código(ASCII), são suas limitações. Com isso o ISO(International Standards Organization)decidiu criar algumas alterações nele para adicionar um padrão de códigos europeus chamado de Latim-1. Microsoft Windows foi modificado e com isso surgiu o ANSI para Windows.
No entanto, por continuar o uso da codificação de 8 bits, ASCII só é capaz de representar 256 símbolos exclusivos, consideravelmente menor do que os símbolos de 10.000 que são comuns em tais linguagens como chinês, coreano e japonês (idiomas orientais). Barreiras de idioma, como ampliar os recursos de computadores além de fontes de maiúsculas, espaçamento mono, os requisitos para um conjunto grande de caracteres exclusivos (por exemplo, letras, pontuação, símbolos técnicos e matemáticos e caracteres de publicação) também têm crescido muito além os recursos do texto de 8 bits.

Para superar as limitações dos outros métodos codificação, várias empresas de computador principal, incluindo Apple Computer, Inc., Sun Microsystems, Inc., Xerox Corp. e IBM (International Business Machines corp.), formado Unicode Inc., um consórcio sem fins lucrativos, para definir o check-out para definir um novo padrão para conjuntos de caracteres internacionais. Ao mesmo tempo, o ISO começou desenvolvendo um padrão. Finalmente, esses padrões mesclado e tornou-se de Unicode. Unicode é publicado como O Unicode Standard, codificação de caractere internacional.

Unicode

Usa codificação de 16 bits que permite 65.536 caracteres distintos. Mais do que suficiente para incluir todos os idiomas em uso atualmente. Além disso, ele oferece suporte vários idiomas de archaic ou hermética, como hieroglyphs sânscrito e Egyptian. Unicode também inclui representações para marcas de pontuação, símbolos matemáticos e dingbats, com espaço deixado para expansão futura. Porque ele estabelece um código exclusivo para cada caractere em cada script, a Windows NT pode garantir que a conversão de caracteres de um idioma para outro seja preciso.

Fonte:
http://support.microsoft.com/kb/99884/pt-br

E-mail/Msn/Orkut: oguh-headshot@hotmail.com


Dúvidas/Sugestões/Idéias/ e Novidades sobre o que virá

Vídeo - Números Binários

Vídeo falando sobre "A importância do sistema decimal binário para a computação eletrônica"

http://www.youtube.com/watch?v=xtjf7prHiDc

Vale a pena conferi-lo!!

Dúvidas/Sugestões/Idéias/ e Novidades sobre o que virá

Tradutor de binários em palavras

Essa mensagem foi criada em binário, mas não temam... pois binários são faceis disponibilizei um tradutor só pra facilitar a vida de vcs ^^

Tradutor:
http://nickciske.com/tools/binary.php

Mensagem do Interligados:
0100000101110110011001010110111001110100011101010111001001100101011011010010110
1011100110110010100100000011100000110010101101100011011110010000001101101011101
0101101110011001000110111100100000011001000110111101110011001000000110001001101
0010110111011100001011100100110100101101111011100110010000001100101001000000110
0100011010010111011001101001011100100111010001100001011011010010110101110011011
0010100101110

Bom divertimento, dúvidas? comentários postem aqui ou então no post para dúvidas

E-mail/Msn/Orkut: oguh-headshot@hotmail.com

Dúvidas/Sugestões/Idéias/ e Novidades sobre o que virá

Tudo no computador são números

Para entender o que a figura acima nos diz, primeiro é preciso saber o conceito de bit e byte. O conceito básico é:

Bit (BInary digiT)

O significado do dicionário é esse: [processamento de dados] s. bit, m.; (1) unidade de medida de informação, com referência ao montante transmitido ou armazenado, pela escolha de um entre dois sinais possíveis; hartley, m.; (2) um dos dígitos do sistema de números binários; (3) um dos pulsos de um grupo de pulsos; abr. de binary digit".

Resumindo, bit é a menor unidade de informação. Os computadores "entendem" impulsos elétricos, positivos ou negativos, que são representados por 1 e 0, respectivamente. A cada impulso elétrico, damos o nome de Bit (BInary digiT). Um bit está para a informação assim como o átomo está para a molécula. Ou seja, o bit é a unidade básica da informação, cujo valor representa duas possibilidades exclusivas.

Byte (BinarY TErm)

[processamento de dados] s. byte, m.; octeto, m.

Em outras palavras, byte é o conjunto formado por 8 bits(octeto). É usado com frequência para especificar o tamanho ou quantidade da memória ou da capacidade de armazenamento de um computador. Só pra complementar a informação, a metade de um byte chama-se nibble ou semiocteto.

Entendendo a Figura

Quando você vê as letras do alfabeto na tela de um computador, está vendo apenas uma maneira de representar os números. Vejamos a seguinte frase:

Eis algumas palavras

O Computador entende assim:

0100010101101001011100110010000001100001011011000110011101110101

0110110101100001011100110010000001110000011000010110110001100001

01110110011100100110000101110011

* Vocês podem conferir no link deixado pelo Hugo num post anterior e que segue abaixo

http://nickciske.com/tools/binary.php

Nesta versão binária da frase "Eis algumas palavras", cada par de quatro digitos representa o código numérico de um caracter. Por exemplo, 0100 0101 é a representação de 69 na base binária, e representa também um "E" na tabela ASCII(tabela muito utilizada utilizada para a troca de informações, nela cada caracter é presentado por 2 pares de nibbles,ou seja, 4 bits + 4 bits = 1 byte ). ASCII significa: American Standard Code for Information Interchange, que em português significa "Código Padrão Americano para o Intercâmbio de Informação".

Existem duas tabelas ASCII: a de 7 bits (com um total de 128 caracteres) e a de 8 bits (com um total de 256 caracteres, que é o padrão estendido incluindo caracteres acentuados). Abaixo segue um link com um programa que contém a tabela ASCII de 8 bits para download. O programa, segundo o próprio autor, foi feito para facilitar o trabalho na hora de incluir algum caracter do tipo "§ ½ ² ³ ª º ç" em algum texto quando o teclado está desconfigurado. Programinha fácil de se usar e ajuda muito.

http://www.richard.eti.br/downloads/ascii.zip

Enfim, espero que tenham entendido o porque do título do post ser "Tudo no computador são números!".

Qualquer dúvida, sugestão ou reclamação, deixem um comentário ou enviem um e-mail pra mim.

e-mail: ivangoleiro@hotmail.com


Referências:

http://www.richard.eti.br/duvidas47.html
http://www.macsystemeduc.com.br/livros/ex17/exemplo17.html
http://translation.babylon.com/English/to-Portuguese/
http://www.dainf.ct.utfpr.edu.br/~robson/prof/aulas/common/bases.htm#info




Dúvidas/Sugestões/Idéias/ e Novidades sobre o que virá

Relógio Binário

Andei procurando coisas interessantes sobre o assunto e descobri um relógio binário. Então decidi mostrá-lo a vocês:



Coluna da Esquerda significam as horas, a do meio minutos e a da direita segundos.
Horas(esquerda)
C1___C2
128__8
64___4
32___2
16___1
Minutos(meio)
C1___C2
128__8
64___4
32___2
16___1
Segundos(direita)
C1___C2
128__8
64___4
32___2
16___1

Podem ser representados em Binários ou BCD, para vê-los em binários clique com o botão direito nele "Settings" e desative "BCD digits instead of binary"

OBS: Ele eh Shareware, depois de um determinado tempo aparece "PLEASE REGISTER" mas é possível observar o relógio em si.

http://www.baixaki.com.br/download/scotts-binary-clock.htm

Legenda:
C1 = Coluna 1
C2 = Coluna 2

E-mail/Msn/Orkut: oguh-headshot@hotmail.com

Dúvidas/Sugestões/Idéias/ e Novidades sobre o que virá